Security & Authentication Protocols

A security protocol is a fixed pattern of exchanges (steps) between 2 or more communication parties to achieve a security related task.

Diffie-Hellman-Merkel Key Exchange Protocol

For brevity sake, I will refer to it as DHM

We use the DHM protocol when two parties wish to communicate privately, but the communication channel is not secure (everything can be read by outsiders), and they want to use secret key encryption.

To do so, A and B have to first publicly agree on values for y and p in a modular exponentiation one way function: \(y^x \!\!\mod p\)

• \(y\) needs to be the primitive root of \(p\)
• \(p\) is an enormously large prime number
• The two numbers can be publicly known

A and B choose secret numbers, \(a\) and \(b\) respectively, then:

• Put \(a\) into the one-way function and computes the result \(y^a \!\!\mod p = v_A\)
• A sends \(v_A\) to B and receives \(v_B\) from B
• A applies their function to \(v_B\): \((v_B)^a \!\!\mod p\)
• B does the same with \((v_A)^b \!\!\mod p\), where \(b\) is B’s secret number.

A and B will arrive at the same value which they use as their secret key \(s\). \((v_A)^b \!\!\mod p = (v_B)^a \!\!\mod p = s\)

Authentication Protocol

Normally when working in a local environment (secure channel) with a fixed link to the host, we use passwords to authenticate a user. However, more must be done over insecure channels.

Either use encrypted passwords, digital signature, or public key encryption for authentication.

Recall how public keys can be used to ensure integrity and non-repudiation, provided that the public key is trusted. Why can’t it provide authentication as well?

Replay Attack

Let’s say A sends B a message encrypted by KU_A, B acknowledges that A is in fact A. However E also stores this message but does not touch it. After the communication with A and B is over, E can replay the message to B and B would accept E as A.

Solution 1. B generates a token R, which is a random number (also called a nonce :eyes: ), that A needs to sign for authentication. The final authenticated token, if it contains a digital signature that is encrypted with A’s private key can only mean it was authenticated by A and B can verify this by decrypting it with A’s public key.

The interaction can be formalised with the notation below.

1. A → B : A
2. B → A : R
3. A → B : [R]_A

Solution 2. Timestamping. When A sends message to B, they include a timestamp in the encrypted message. If the message is replayed by E, B will know that it is an old message.

Mutual Authentication

Our above examples are a unilateral authentication: A authenticates B but not the other way around.

Mutual authentication. Two-way authentication

1. A → B : A, R_A
2. B → A : R_B, [R_A]_B (In this step, A will know that B is truly B – as long as public key verified)
3. A → B : [R_B]_A (Here B, will know A is A)

Authentication with DS vs Encryption

Using digital signature:

1. A → B: “I’m Alice”
2. B → A: R (Bob’s token)
3. A → B : [R]_Alice (Bob’s token signed by A)

Using public key encryption:

1. A → B: “I’m Alice”
2. B → A: {R}_KPAlice
3. A → B: R

This achieves a similar effect to DS.

Authentication Spoofing

There’s still a problem with our protocol. A could communicate with E, but E could be malicious and decide to pass on the message to B. Now B will pass the token to E and E passes it to A and then passes the encrypted token back to B from A.

As a result, B thinks that they are communicating with A.

This is often referred to as a “man-in-the-middle” (MITM) attack

The main idea behind the two solutions are to include information about both the sender and the receiver during communication. Depending on which method we are using to authenticate (DS or Public key Encryption), we include the missing information.

TLDR.

• When using encryption, sender’s id is included.
• When using digital signature, receiver’s id is included

Solution 1. Include the identity of the intended recipient encrypted along with the hash of the token from the recipient because information of the sender is the digital signature.

1. A → B: A
2. B → A: R
3. A → B: [R, E]_A 🔔❕❗

Solution 2. If we’re using encryption for authentication (Needham-Schroeder Authentication protocol), enclose the sender’s ID (B below) because receiver’s info is that the message was encrypted with their public key.

1. A → B: A
2. B → A: {B, R}_KPA
3. A → B: R

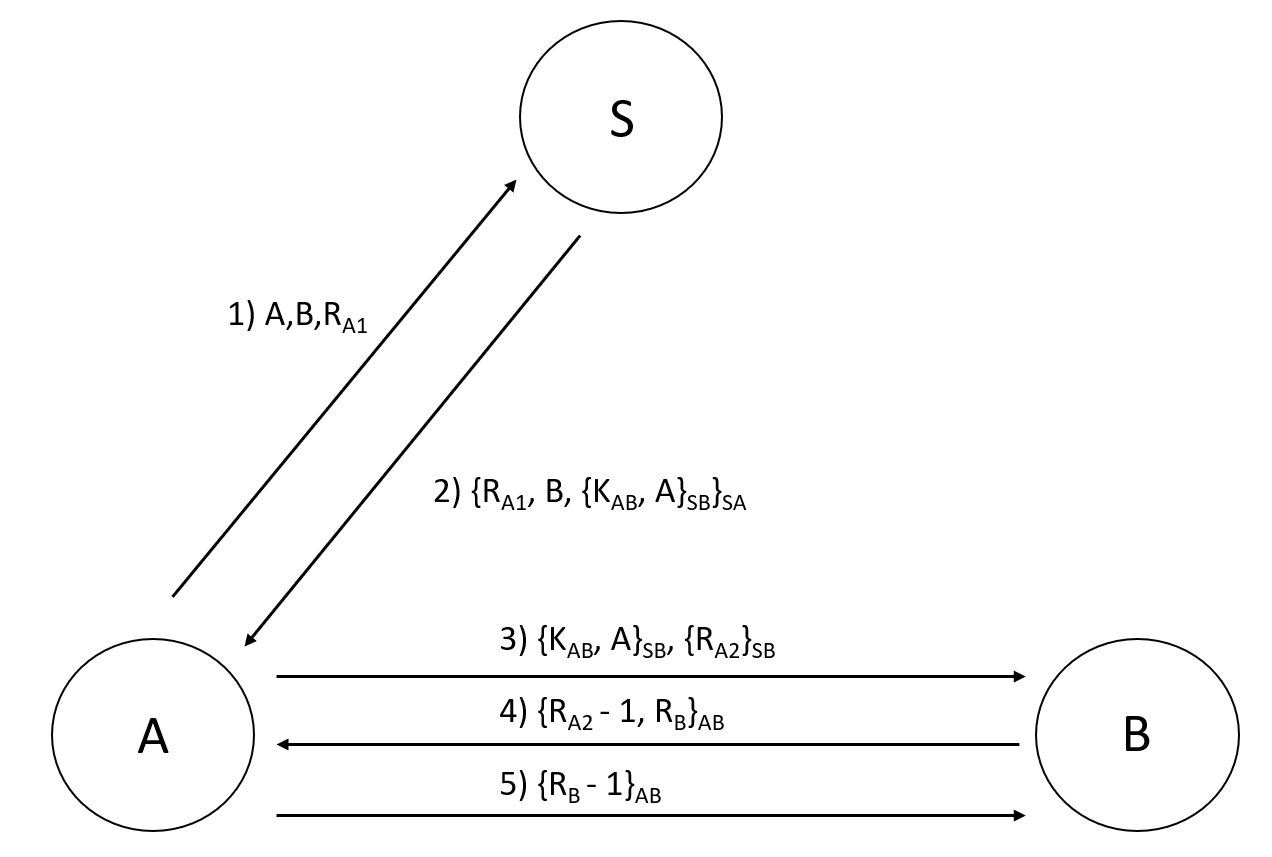
Needham-Schroeder Secret key-based protocol

We saw the public key encryption protocol by NS, they also proposed a secret key authentication protocol. In this protocol, there are 3 parties: A (K_SA – key given to A by server), B (K_SB – key given to B by server), Server (K_AB – session key that server provides to both A and B)

1. A → S: A, B, R_A1
2. S → A: { R_A1, B, { K_AB, A }_KSB }_KSA
3. A → B: { K_AB, A }_KSB, { R_A2 }_KAB
4. B → A: { R_A2 – 1, R_B}_KAB
5. A → B: { R_B – 1 }_KAB

Disadvantages. Server needs to distribute secret key directly to B, and since B does not ask for a key, but receives one, if B is not responsive (AFK) or the server somehow can’t reach B then there will be no communication.

Possible Attack

If E manages to obtain an old session key, K_AB, E can replay the old message (step 3) relating to that session key.

• If B completes the protocol and assumes that they shared a key with A, E would have tricked B.
• Can prevent this easily with timestamps.